05. Transposed Convolutions

Transposed Convolutions

Transposed Convolutions help in upsampling the previous layer to a higher resolution or dimension. Upsampling is a classic signal processing technique which is often accompanied by interpolation. The term transposed can be confusing since we typically think of transposing as changing places, such as switching rows and columns of a matrix. In this case when we use the term transpose, we mean transfer to a different place or context.

We can use a transposed convolution to transfer patches of data onto a sparse matrix, then we can fill the sparse area of the matrix based on the transferred information. Helpful animations of convolutional operations, including transposed convolutions, can be found here. As an example, suppose you have a 3x3 input and you wish to upsample that to the desired dimension of 6x6. The process involves multiplying each pixel of your input with a kernel or filter. If this filter was of size 5x5, the output of this operation will be a weighted kernel of size 5x5. This weighted kernel then defines your output layer.

Methods of upsampling

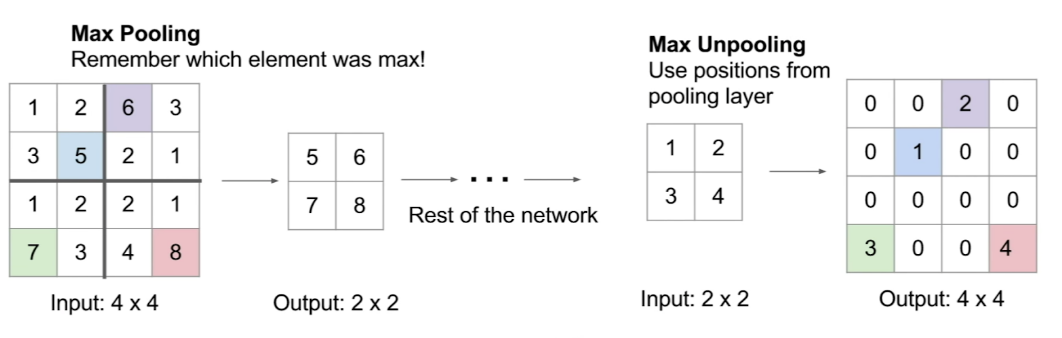
1. Max "unpooling"
2. Learnable upsampling (with transposed convolutions)

The first is pictured below.

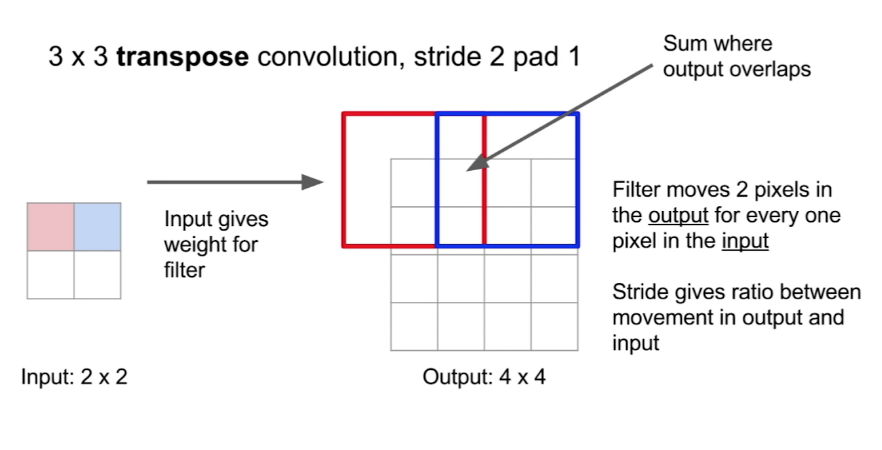
Learnable upsampling, transposed convolutions

We've been going over learnable upsampling layers. The upsampling part of the process is defined by the strides and the padding. Let's look at a simple representation of this. If we have a 2x2 input and a 3x3 kernel and a stride of 2, we can expect an output of dimension 4x4. The following image gives an idea of the process.